Let
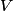 and and 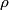 denote the volume and density of the block, respectively. From Archimedes' Principle, the buoyant force due to the water is denote the volume and density of the block, respectively. From Archimedes' Principle, the buoyant force due to the water is 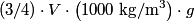 and the buoyant force to the oil is 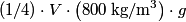 So, the total buoyant force is 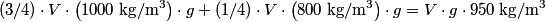 This must equal the weight of the block, 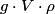 , so , so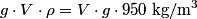 Thus, 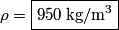 Therefore, answer (C) is correct. |